求一致最小方差无偏估计的方法

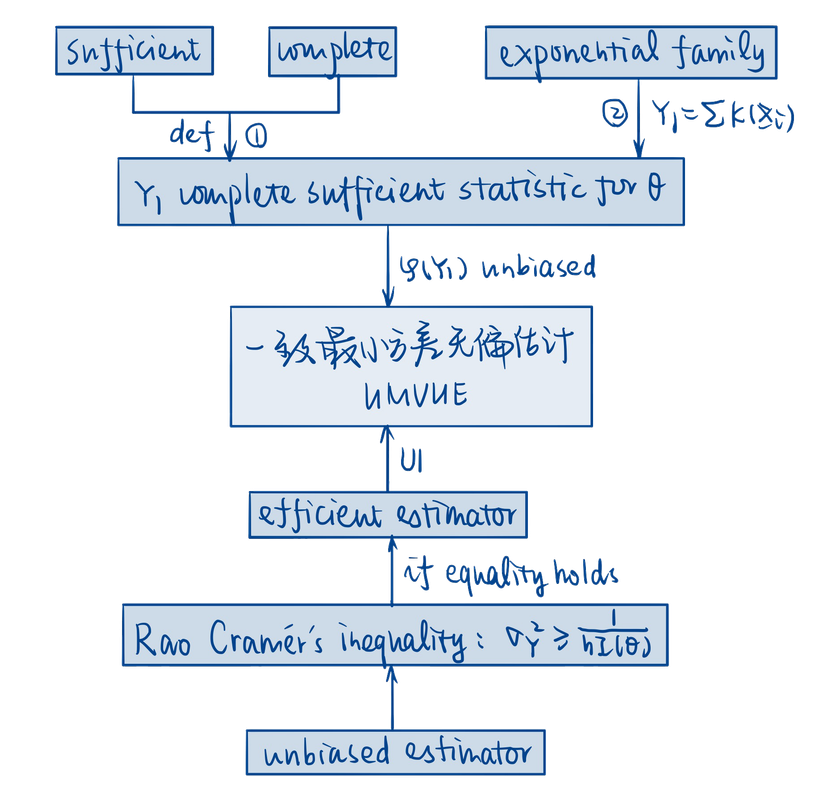
该部分内容对应Hogg课本的第7-8章，主要讨论构造一致最小方差无偏估计(UMVUE)的两种思路，一种是通过构造充分完备统计量的函数，另一种则是通过构造有效估计量。

一、充分完备统计量

概念1: 充分统计量

定义1. 称$Y_1=u(X_1,X_2,\cdots,X_n)$为$\theta$的充分统计量(sufficient statistic)，如果

$$
\frac{f(x_1;\theta)f(x_2;\theta) \cdots f(x_n;\theta)}{g_1(u(x_1,x_2,\cdots,x_n);\theta)} = H(x_1,x_2,\cdots,x_n)
$$

不依赖于$\theta \in \Omega$.

例1. 设$X \sim \Gamma(2,\theta)$，$Y_1=X_1+X_2+\cdots+X_n$，证明$Y_1$是关于$\theta$的充分统计量.

证明: 由于$X$的矩母函数为$M_X(t)=E[e^{tX}]=(1-\theta t)^{-2}, t<1/\theta$，所以

$$
M_{Y_1}(t)=E[e^{t\sum X_i}]=(1-\theta t)^{-2n} \Rightarrow Y_1 \sim \Gamma(2n,\theta)
$$

根据以上定义，

$$
\begin{aligned}
\frac{f(x_1;\theta)f(x_2;\theta) \cdots f(x_n;\theta)}{g_1(y_1;\theta)} &= \frac{\prod\limits_{i=1}^n \frac{1}{\Gamma(2)\theta^2} x_ie^{-x_i/\theta}}{\frac{1}{\Gamma(2n)\theta^{2n}}(\sum x_i)^{2n-1}e^{-\sum x_i/\theta}} \\\
&=\frac{\Gamma(2n)}{\Gamma(2)^n}\frac{\prod_{i=1}^n x_i}{(\sum x_i)^{2n-1}}
\end{aligned}
$$

等式右端不依赖于$\theta$，所以$Y_1$是关于$\theta$的充分统计量. $\square$

定理1 (Factorization Thm). $Y_1=u(X_1,X_2,\cdots,X_n)$为$\theta$的充分统计量 $\Leftrightarrow$ 存在非负函数$k_1,k_2$使得

$$
f(x_1;\theta)f(x_2;\theta) \cdots f(x_n;\theta)=k_1[u(x_1,x_2,\cdots,x_n);\theta] \cdot k_2(x_1,x_2,\cdots,x_n)
$$

其中$k_2$不依赖于$\theta$.

例2. 题设同例1，利用因子分解定理：

$$
\begin{aligned}
f(x_1;\theta)f(x_2;\theta) \cdots f(x_n;\theta)&=\prod_{i=1}^n \frac{1}{\Gamma(2)\theta^2} x_ie^{-x_i/\theta}\\ &=\frac{1}{\Gamma(2n)\theta^{2n}} \left( \prod_{i=1}^n x_i \right) e^{-\sum x_i/\theta}
\end{aligned}
$$

设

$$
k_1[u(x_1,x_2,\cdots,x_n);\theta]=\frac{1}{\Gamma(2n)\theta^{2n}}e^{-\sum x_i/\theta}, \\ \quad k_2(x_1,x_2,\cdots,x_n)=\prod_{i=1}^n x_i
$$

其中$k_2$不依赖于$\theta$，所以$Y_1$是关于$\theta$的充分统计量. $\square$

性质1. 设$Y_1=u_1(X_1,X_2,\cdots,X_n)$是$\theta$的充分统计量，则

• 若$\theta$存在唯一的最大似然估计$\hat{\theta}$，则$\hat{\theta}$是关于$Y_1$的函数；
• 若$u$为可逆函数，则$Z_1=u(Y_1)$仍是$\theta$的充分统计量；
• (Rao-Blackwell) 设$Y_2=u_2(X_1,X_2,\cdots,X_n)$是$\theta$的一个无偏估计量，且$Y_2$不是以$Y_1$为单一变量的函数，则统计量$\varphi(Y_1)=E[Y_2|Y_1]$是$\theta$的无偏估计量，且满足$\operatorname{var}[\varphi(Y_1)] \leq \operatorname{var}[Y_2]$.

概念2: 完备分布族

定义2. 设$Z$为连续型或离散型随机变量，其密度函数属于分布族$\{h(z,\theta):\theta\in\Omega\}$，称该分布族是完备的(complete)，如果对任意$\theta\in\Omega$，$E[u(Z)]=0 \Rightarrow u(z) \equiv 0$ a.s.

定理2. 设$Y_1=u_1(X_1,X_2,\cdots,X_n)$是$\theta$的充分统计量，且$\{g_1(y_1;\theta):\theta\in\Omega\}$是完备分布族. 若$E[\varphi(Y_1)]=E[\psi(Y_1)]=\theta$，则$\varphi(Y_1)=\psi(Y_1)$ a.s.，在此意义下，$\varphi(Y_1)$是$\theta$的唯一最小方差无偏估计.

例3 (ex 7.26). 考虑分布族$\{h(z,\theta)=\frac{1}{\theta},0<z<\theta;\theta \in \Omega\}$

(a) 证明当$\Omega=\{\theta:0<\theta<\infty\}$时，该分布族是完备的；

(b) 证明当$\Omega=\{\theta:1<\theta<\infty\}$时，该分布族不完备.

证明: (a) 设$Z \sim h(z,\theta)$，其中$h(z,\theta)$属于该分布族. 不妨设$u(z)$为可积函数（事实上可测即可）且其原函数为$U(z)$，若$u(z)$满足

$$
0=E[u(Z)]=\int_0^{\theta} u(z) \cdot \frac{1}{\theta} \mathrm{d}z, \quad \forall \theta>0
$$

等式两边同乘$\theta$得到

$$
0=\int_{0}^{\theta} u(z) \mathrm{d}z = U(\theta)-U(0), \quad \forall \theta>0
$$

于是$U(z) \equiv C (\forall , 0<z<\theta) \Rightarrow u(z)=U’(z)=0$ a.s.

(b) 设$Z \sim h(z,\theta)$，其中$h(z,\theta)$属于该分布族. 令

$$
u(z) := \left\{
\begin{aligned}
&1 \quad , 0<z<1/2 \\
&-1 , 1/2 \leq z < 1 \\
&0 \quad , 1 \leq z < \theta
\end{aligned}
\right.
$$

为非零值函数，则有

$$
\begin{aligned}
E[u(Z)] &= \int_0^{\theta} u(z) \cdot \frac{1}{\theta} \mathrm{d}z \\
&= \frac{1}{\theta} \left( \int_0^{1/2} 1 \mathrm{d}z + \int_{1/2}^{1} (-1) \mathrm{d}z + \int_1^{\theta} 0 \mathrm{d}z \right) \\
&= \frac{1}{\theta} \left( \frac{1}{2}-\frac{1}{2}+0 \right) = 0 , \quad \forall 1<\theta<\infty
\end{aligned}
$$

由定义可知，该分布族不完备. $\square$

概念3: 指数分布族

定义3. 设$\Omega=(\gamma,\delta)$，连续型密度函数构成的分布族$\{f(x;\theta):\theta\in\Omega\}$称为指数分布族(exponential class)，如果$f(x;\theta)$具有如下规范形式(regular case)：

$$
f(x;\theta)=\exp\{p(\theta)K(x)+S(x)+q(\theta)\}, \quad x \in \mathscr{A}=(a,b)
$$

其中 (1) $\mathscr{A}=(a,b)$与$\theta$无关；

(2) $p(\theta)$是$\theta$的非平凡（即$p(\theta) \not\equiv C$）连续函数；

(3) $K’(x) \not\equiv 0$和$S(x)$都是$x$的连续函数.

定义4. 设$\Omega=(\gamma,\delta)$，离散型密度函数构成的分布族$\{f(x;\theta):\theta\in\Omega\}$称为指数分布族，如果$f(x;\theta)$具有如下规范形式：

$$
f(x;\theta)=\exp\{p(\theta)K(x)+S(x)+q(\theta)\}, \quad x=a_1,a_2,\cdots
$$

其中 (1) $\{x:x=a_1,a_2,\cdots\}$与$\theta$无关；

(2) $p(\theta)$是$\theta$的非平凡连续函数；

(3) $K(x)$是$x$的非平凡函数.

定理3. 若随机样本$X_1,X_2,\cdots,X_n$的密度函数$f(x;\theta),\gamma<\theta<\delta$属于指数分布族且具有规范形式

$$
f(x;\theta)=\exp\{p(\theta)K(x)+S(x)+q(\theta)\}
$$

则$Y_1=\sum_{i=1}^n K(X_i)$是$\theta$的充分统计量，且$\{g_1(y_1;\theta),\gamma<\theta<\delta\}$是完备分布族，即$Y_1$是$\theta$的充分完备统计量(complete sufficient statistic).

推论4. 设$Y_1$是$\theta$的充分完备统计量，若$\varphi(Y_1)$满足$E[\varphi(Y_1)]=\theta$，则$\varphi(Y_1)$是$\theta$唯一最小方差无偏估计.

例4 (ex 7.39). 设随机样本$X_1,X_2,\cdots,X_n, ; n>2$服从二项分布$b(1,\theta)$.

(a) 证明$Y_1=\sum X_i$为$\theta$的充分完备统计量；

(b) 求$\theta$的一致最小方差无偏估计$\varphi(Y_1)$；

(c) 令$Y_2=(X_1+X_2)/2$，计算$E[Y_2]$；

(d) 计算$E[Y_2|Y_1=y_1]$.

证明: (a) 由于$X_i$的密度函数

$$
f(x;\theta)=\theta^x(1-\theta)^{1-x}=\exp\Bigg\{ \overbrace{\ln \frac{\theta}{1-\theta}}^{p(\theta)} \cdot \underbrace{x}_{K(x)} + \overbrace{0}^{S(x)} + \underbrace{\ln(1-\theta)}_{q(\theta)} \Bigg\}, \quad x=0,1
$$

为满足以上(1)(2)(3)条件的规范形式，所以$\{f(x;\theta)\}$为指数分布族，于是$Y_1=\sum K(X_i)=\sum X_i$为$\theta$的充分完备统计量.

(b) 由于$Y_1 \sim b(n,\theta)$，所以$E[Y_1]=n\theta$. 于是当我们令$\varphi(Y_1)=\frac{1}{n}Y_1$，则$E[\varphi(Y_1)]=\theta$，且$\varphi(Y_1)$为$\theta$的一致最小方差无偏估计.

(c) $E[Y_2]=\frac{E[X_1]+E[X_2]}{2}=\frac{\theta+\theta}{2}=\theta$.

(d) 由于$Y_1$为充分统计量，$Y_2$为无偏估计量，由Rao-Blackwell定理可知$E[Y_2|Y_1=y_1] \equiv \psi(y_1)$也是无偏估计量，即$E[\psi(y_1)]=\theta$. 于是显然$\psi(y_1)=\varphi(y_1)=\frac{1}{n}y_1$，从而$E[Y_2|Y_1=y_1]=\psi(y_1)=\frac{1}{n}y_1$. $\square$

定理5. 若随机样本$X_i$的密度函数$f(x;\theta)$满足规范形式，则

$$
E[K(X_i)] = -\frac{q’(\theta)}{p’(\theta)},
$$

如果设$Y_1=\sum K(X_i)$，则

$$
E[Y_1]=\sum E[K(X_i)]=-n\frac{q’(\theta)}{p’(\theta)}.
$$

事实上，这直接给出了指数分布族中充分完备统计量的数学期望.

总结

Rao-Blackwell定理告诉我们可以利用充分统计量使无偏估计量的方差逐步缩减，但实际上我们并不需要从无偏估计量出发，而是通过构造充分完备统计量直接求得UMVUE，另外指数分布族的引入也极大地方便了充分完备统计量的构造.

二、有效估计量

定义4. 随机变量$X$的Fisher信息量(Fisher information)定义为

$$
I(\theta)=E\left[\left(\frac{\partial \ln f(X;\theta)}{\partial \theta}\right)^2\right]=-E\left[\frac{\partial^2 \ln f(X;\theta)}{\partial \theta^2}\right]
$$

随机样本$(X_1,X_2,\cdots,X_n)$的Fisher信息量定义为

$$
I_n(\theta)=nI(\theta)
$$

一般来说，上述第二种表达式更容易计算.

定理6 (Rao-Cramer inequality). 设$Y=u(X_1,X_2,\cdots,X_n)$是$\theta$的无偏估计量，则$Y$的方差$\sigma_Y^2:=\operatorname{var}[Y]$满足

$$
\sigma_Y^2=\operatorname{var}[Y] \geq \frac{1}{nI(\theta)}
$$

特别地，若$Y$的方差恰好为Rao-Cramer下界，即

$$
\sigma_Y^2=\operatorname{var}[Y] = \frac{1}{nI(\theta)}
$$

则$Y$是$\theta$的一致最小方差无偏估计量.

定义5. 设$Y$是$\theta$的无偏估计量，称$Y$是$\theta$的有效估计量(efficient estimator)，若$Y$的方差达到Rao-Cramer下界，即

$$
\sigma_Y^2=\operatorname{var}[Y] = \frac{1}{nI(\theta)}
$$

注： {有效估计量} $\subset$ {UMVUE}

定义6. 设$Y$是$\theta$的无偏统计量，定义其功效(efficiency)为Rao-Cramer下界 $\frac{1}{nI(\theta)}$与$Y$的方差$\sigma_Y^2$的比值，即

$$
\text{efficiency of } Y := \frac{1}{nI(\theta) \cdot \sigma_Y^2} \leq 1
$$

特别地，$Y$为有效估计量，当且仅当$\text{efficiency of } Y = 1$.

例5 (ex 8.15). 设$X \sim \Gamma(4,\theta)$，其中$\theta>0$.

(a) 求Fisher信息量$I(\theta)$；

(b) 设随机变量$X_1,X_2,\cdots,X_n$服从该分布，证明$\theta$的最大似然估计为有效估计量.

证明: (a) 由于$X \sim \Gamma(4,\theta)$，则有

$$
\begin{aligned}
f(x;\theta)=\frac{1}{6\theta^4} x^3 e^{-\frac{x}{\theta}}
&\Rightarrow \ln f(x;\theta)=3\ln x-\frac{x}{\theta}-\ln \Gamma(4)-4\ln \theta \\
&\Rightarrow \frac{\partial \ln f(x;\theta)}{\partial \theta} = \frac{x}{\theta^2} - \frac{4}{\theta} \\
&\Rightarrow \frac{\partial^2 \ln f(x;\theta)}{\partial \theta^2} = -\frac{2x}{\theta^3}+\frac{4}{\theta^2}
\end{aligned}
$$

所以$I(\theta)=\frac{2}{\theta^3}E[X]-\frac{4}{\theta^2}=\frac{4}{\theta^2}$.

(b) 易求得$\theta$的最大似然估计为$\hat{\theta}=\frac{1}{4}\overline{X}$，由于

$$
\operatorname{var}[\hat{\theta}] = \frac{1}{16} \operatorname{var}[\overline{X}] = \frac{1}{16} \cdot \frac{4\theta^2}{n} = \frac{\theta^2}{4n} = \frac{1}{nI(\theta)}
$$

所以$\hat{\theta}$为$\theta$的有效估计量. $\square$

参考文献

1. Hogg, R. V., & Craig, A. T. (. T. (1995). Introduction to mathematical statistics (5th ed.). Englewood Cliffs, N.J.: Prentice Hall.